Olivier Decourt
ABS Technologies / Educasoft Formations
Séminaire DataMining Educasoft
1- Les principes
La robustesse, un premier exemple :
Quelle confiance avoir dans cette droite si je rajoute de nouveaux individus ?
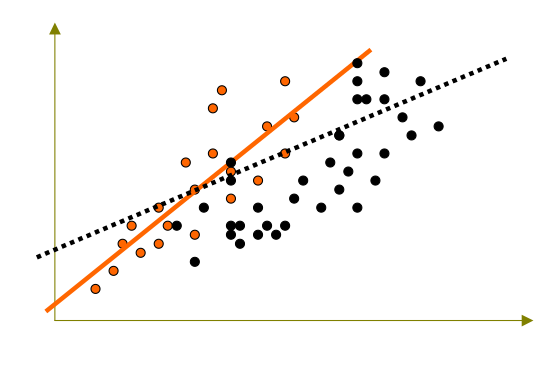
La robustesse, un deuxième exemple :
2 groupes d’individus distincts : toute modélisation de l’ensemble sera médiocre.
2 modèles séparés : meilleure précision.

La robustesse, une définition : « Qualité des modèles qui ne perdent pas en performance si on les applique à de nouveaux individus. »
Un modèle robuste est donc loisible de bien prédire le comportement de nouveaux clients.
Les modèles stratifiés
On isole des sous-populations ayant de fortes ressemblances ; on modélise séparément dans chacune de ces sous-populations.
Le modèle global fait la synthèse (la somme) des différents « sous-modèles » obtenus.
Avantages :
- Simplicité de l’idée
- Lisibilité du modèle
- Convient bien à tous les cas étudiés
Inconvénients :
- Représentativité de l’échantillon de travail ?
- Difficulté de séparer les individus en classes homogènes et stables
Les modèles itératifs
« Cent fois sur le métier remettra ton ouvrage »
On fait la modélisation un grand nombre de fois sur des populations légèrement différentes
Toutes ces sous-populations sont issues de la population d’origine (pas de nouveaux individus).
Le modèle final est une synthèse (une moyenne) des différents modèles obtenus.
Plusieurs variantes :
- le Jackknife (population à modéliser moins 1 individu)
- le Bootstrap simple (échantillonnage à probabilités égales dans la population à modéliser)
- le Bootstrap à probabilités inégales (variante du précédent : l’échantillon n’est pas représentatif de la population de départ)
Les modèles itératifs : principe
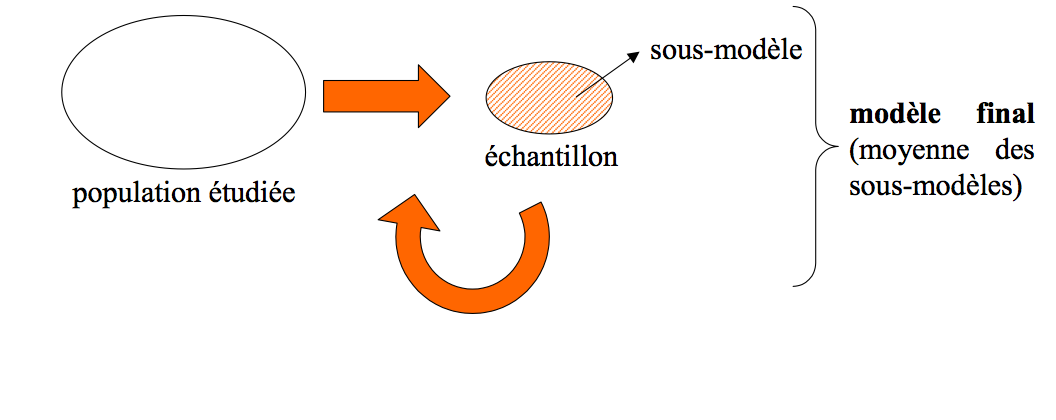
Avantages :
- Grande robustesse du modèle final
- Possibilité de connaître l’imprévisibilité du modèle
Inconvénients :
- Temps d’exécution !
- Programmation parfois plus ardue
- Comment faire la synthèse de certains modèles ?
Le Jackknife
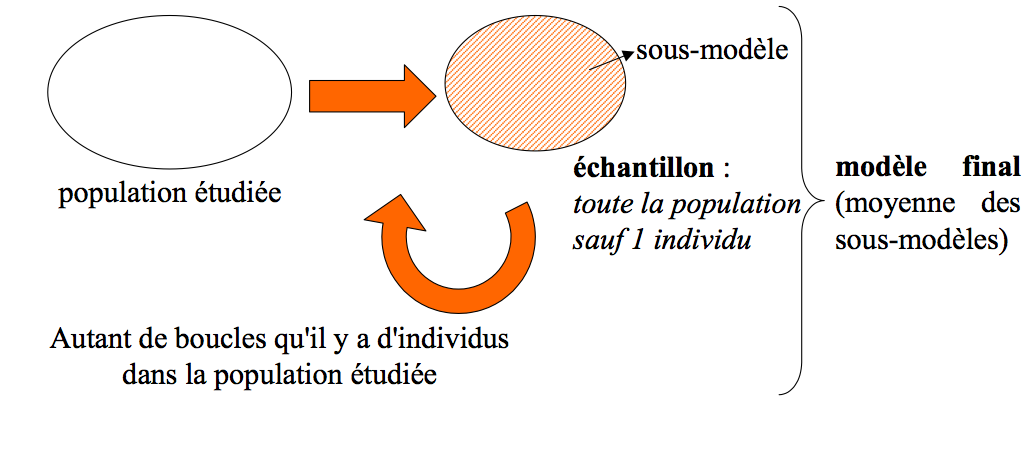
Le Bootstrap
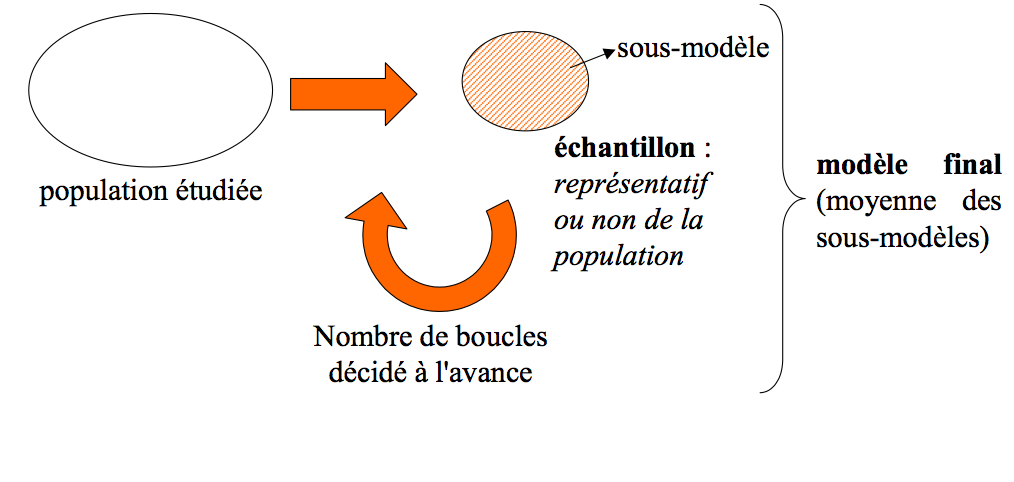
Le Bootstrap : échantillonnage
Sondage à probabilités égales
- Respecter la population
- Chaque individu de la population a la même probabilité d’appartenir à l’échantillon
Sondage à probabilités inégales
- On impose a priori des probabilités d’inclusion ! : sur-représentation de certains individus
Importance de cette étape : gain de temps !
Un premier exemple : Les vins de France de 1969 à 1985
Un 1er modèle pour le Bourgogne rouge :
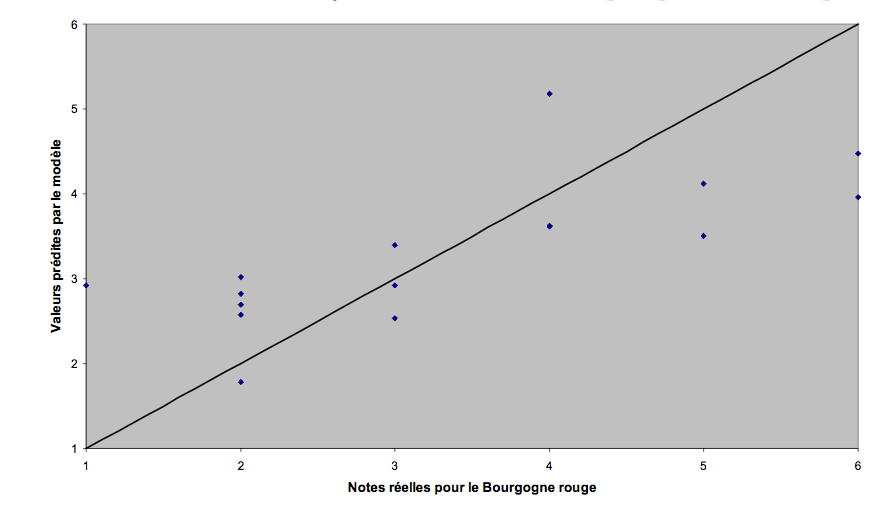
Un modèle stratifié pour le Bourgogne rouge
1. Classification des années (PROC FASTCLUS) sur la base des données météos
2. Stratification selon cette variable de classe (2 classes créées)
Modèle stratifié pour le Bourgogne rouge :
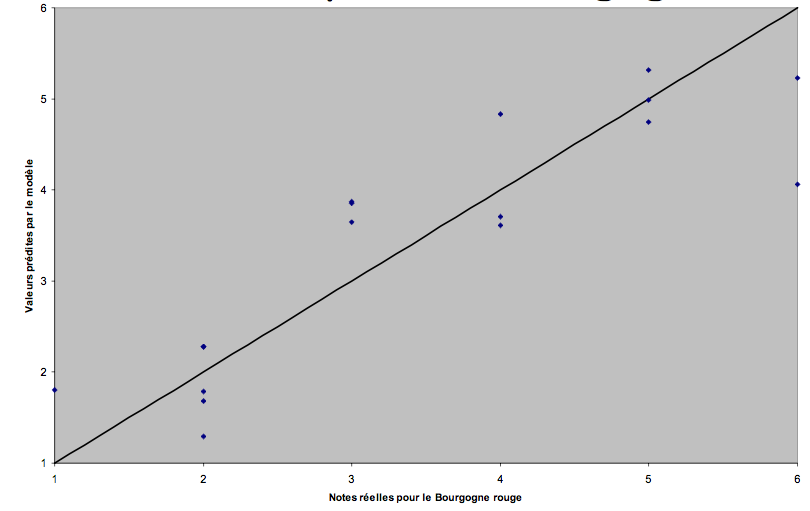
Comparaison des deux modèles :
Modèle simple : SCE = 14,81
Modèle stratifié : SCE = 8,79
On a donc presque diminué de 40 % (!) la distance moyenne entre les valeurs réelles et les valeurs prévues
Note : SCE = Somme des Carrés des Ecarts
Jackknife et Bootstrap à probabilités égales sur le modèle non stratifié
On procède, selon les cas, à 17 boucles (Jackknife) ou à seulement 10 boucles (Bootstrap à probabilités égales).
Performance des modèles itérés :
- SCE du Jackknife : 14,05
- SCE du Bootstrap (en moyenne) : 7,70
(La SCE du bootstrap est comprise entre 8,89 et 6,14 sur 30 essais.)
Pour mémoire :
- SCE du modèle normal : 14,81
- SCE du modèle stratifié : 8,79
Que constate-t-on ?
- Modèle robuste à « meilleur » modèle
- Jackknife : une seule observation peut tout changer
- Bootstrap : meilleur moyen de niveler les effets des observations atypiques si on prend les « bons » échantillons !
Autre avantage des modèles itérés : les intervalles de confiance :
Bootstrap sur le modèle simple :
- Le coefficient de la température minimale est compris entre -0,38 et -0,44 (avec 95% de chances de tomber juste dans cet intervalle).
- La valeur moyenne s’établit à -0,41.
- Le modèle sans itération propose une valeur de -0,37.
Mise en oeuvre sous SAS
Avec des macro-programmes :
Les modèles stratifiés, le Jackknife et le Bootstrap à probabilités égales sont assez faciles à développer.
Avec SAS Enterprise Miner :
Possibilité de modèles stratifiés et de Bootstrap, sauf la partie « intervalle de confiance » du modèle Noeuds GROUP PROCESSING et ENSEMBLE
Un exemple « DataMining » : « Qualité » des clients d’une assurance automobile
Les données
20020 clients d’une assurance automobile décrits par 21 variables :
- âge de l’assuré
- marque de la voiture
- bonus / malus
- âge du véhicule
- année du permis
- situation familiale …
connus comme « bons » ou « mauvais » clients.
La problématique :
Construire un score à partir des renseignements existants pour repérer les bons et les mauvais clients parmi de nouveaux candidats à l’assurance.
Le modus operandi :
On testera la qualité et la robustesse de nos modèles en les construisant sur 10000 clients, et en « scorant » les 10020 restants, inconnus jusqu’alors.
Premier modèle
Une régression logistique (puisque la variable à modéliser est binaire) avec 11 variables explicatives :
- usage du véhicule, est-il dans un garage fermé ?
- âge, puissance et valeur du véhicule
- année du permis, situation familiale, âge, ancienneté du contrat et CRM de l’assuré
- nombre de sinistres de l’année écoulée
Taux de confusion : 19,36 %

Le Bootstrap avec SAS Enterprise Miner
Les ingrédients

La recette
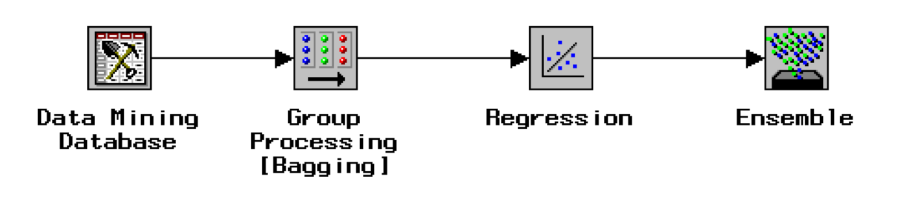
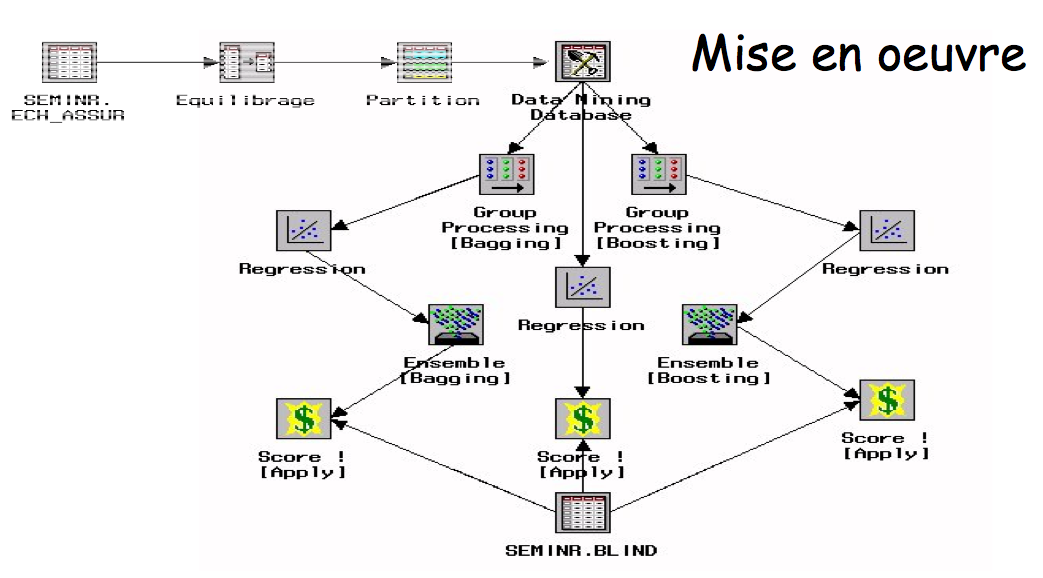

Conclusion
- La robustesse est un des atouts indispensables d’un score : c’est sa capacité de généralisation.
- On la teste avec la partition des données et la validation croisée.
-
On peut accroître la robustesse avec des modèles complexes.
-
La mise au point de ces modèles demande plus de temps, mais leur durée de vie s’accroît également.
-
Un modèle robuste n’est pas forcément meilleur de prime abord !

