Représenter graphiquement la répartition d’un score

Intérêt

Une régression logistique, ou d’autres modèles décisionnels comme les réseaux de neurones, les arbres de décision, les analyses discriminantes, etc., produisent des scores. Ceux-ci sont transformables, selon le problème, en décisions. Si ça doit être le cas, quel seuil doit-on choisir ? Est-ce qu’un score coupé à 0,5 est toujours le meilleur choix ?

Le graphique présenté ici permet d’affiner le choix du seuil de score. Il utilise la procédure KDE, nouveauté de SAS/STAT en version 8.

Type de données requis

Il est nécessaire d’avoir généré une table contenant les prédictions pour des individus dont le statut est connu. Par exemple, avec une procédure LOGISTIC, le code sera le suivant :

PROC LOGISTIC DATA = ... ;
 MODEL cible = ... ;
 OUTPUT OUT = work.predictions P = score ;
 RUN ;

Estimation de la répartition

La procédure KDE va estimer la densité du score produit. C’est à dire qu’elle va produire sa répartition, en « comblant les trous » dus à l’absence de l’intégralité des profils de données qui auraient créé des scores réellement continus.

PROC SORT DATA = work.predictions ;
 BY cible;
 RUN ;
 PROC KDE DATA = work.predictions OUT = work.courbe ;
 VAR score ;
 BY cible ;
 RUN ;

Utilisation

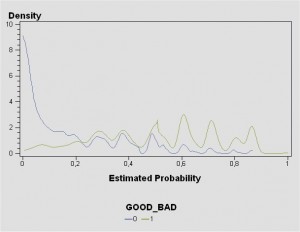
Enfin, la procédure GPLOT produira un graphique semblable à celui-ci…

SYMBOL i = SM20 ;
 PROC GPLOT DATA = work.courbe ;
 PLOT density * score = cible / LEGEND ;
 RUN ; QUIT ;
 Ici, le choix de trois zones de décision sera sans doute approprié :

pour un score entre 0 et 0,2, la décision sera GOOD_BAD = 0 (majoritaires) ;
pour un score entre 0,5 et 1, la décision sera GOOD_BAD = 1 ;
entre 0,2 et 0,5, une zone d’indécision demeurera : les deux populations sont mêlées en proportions égales dans cette portion des scores. La décision sera alors laissée à un opérateur humain.