Le but de cette annexe n’est pas d’expliquer en détail toute la théorie et la pratique des réseaux de neurones, mais seulement d’en définir les principaux termes :
• Neurone
• Poids synaptiques
• Apprentissage
• Réseau de neurones
• Couche cachée
• Linéarité
• Données d’apprentissage et de validation
Principe du neurone artificiel
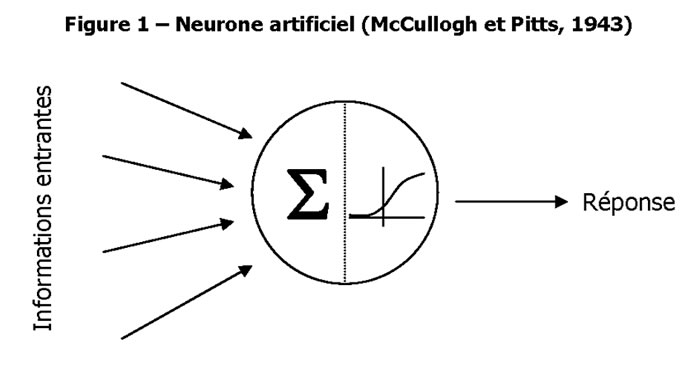
Le neurone artificiel (neurone informatique) est un petit modèle statistique à lui tout seul.
Il doit accomplir deux tâches :
1) la synthèse des informations qui lui sont fournies
et 2) la transformation (souvent non linéaire) de cette information en quelque chose de nouveau.
Ce fonctionnement est présenté sur la Figure 1.
Pourquoi le neurone artificiel est-il un modèle ? Prenons une régression linéaire : les informations entrantes (valeurs des variables explicatives) sont combinées avec des poids (les coefficients du modèle) puis transformées (à l’identique) pour fournir une réponse qui est la valeur prédite par le modèle.
Les coefficients du modèle sont calculés afin que les valeurs prédites soient les plus proches possibles de celles qui sont observées.
Le comportement du neurone artificiel sera assez semblable : il va chercher à ajuster un coefficient associé à chaque information entrante (on parle de poids synaptique) afin de réduire une fonction d’erreur.
La transformation effectuée lors de la seconde phase peut utiliser n’importe quelle fonction mathématique ou presque. Au contraire des poids, cette fonction de transfert (ou d’activation) est choisie à l’avance : elle fait partie des choix architecturaux.
La phase où, par un algorithme itératif, les poids synaptiques vont être modifiés pour trouver un minimum de cette fonction d’erreur s’appelle la phase d’apprentissage.
Les neurones artificiels en réseaux : pourquoi et comment
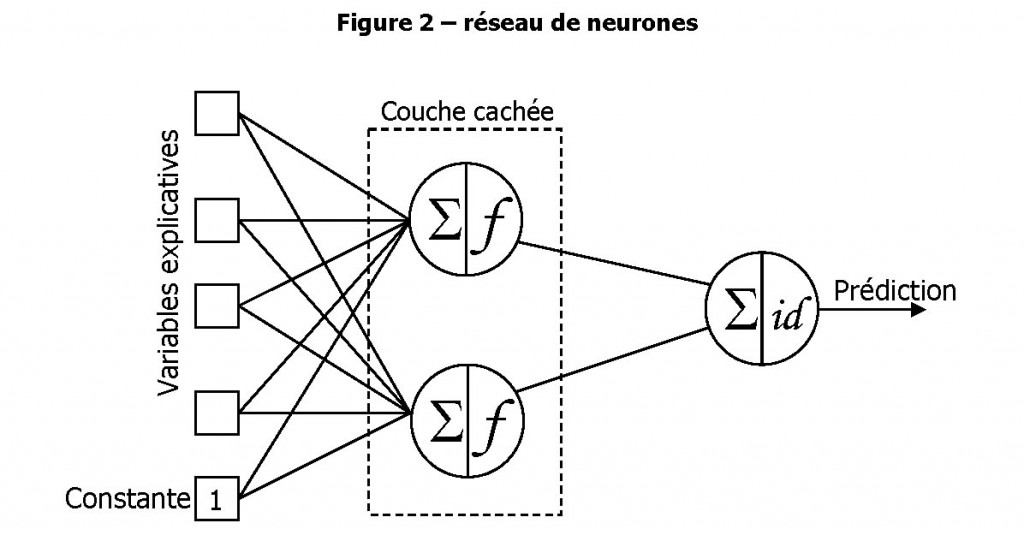
Si chaque neurone pris séparément constitue un modèle, leur mise en réseau (Figure 2) permet d’obtenir un modèle plus complexe.
L’utilisation de fonctions de transfert non linéaires permet de dépasser les limites d’une régression.
L’idée de confronter les données à une série de neurones en parallèle dans une couche cachée permet à la fois de réduire la dimension des informations entrantes (si le nombre de neurones cachés est inférieur au nombre d’entrées, ce qui est presque toujours le cas) et de « solidifier » la prédiction réalisée.
La réduction de dimension permet en particulier de mettre un grand nombre d’informations entrantes dans le modèle sans se soucier de multicolinéarité (redondance des informations) ou d’inutilité d’une information.
La couche cachée est un goulet d’étranglement dont seule l’information pertinente ressortira, combinée et transformée de manière non linéaire, pour faire coïncider les variations des données en entrée avec les variations de la quantité à prédire.
Dans la Figure 2, chaque trait entre les entrées et les neurones de la couche cachée correspond à un poids synaptique, donc à un coefficient du modèle. On voit que par rapport à une régression, par exemple, le nombre de coefficients est largement supérieur dans un réseau de neurones. Une entrée constante (appelée biais) permet de reproduire également un comportement « de base », comme dans une régression.
Le neurone de sortie, le dernier à droite, ne sert qu’à combiner les prédictions des couches cachées en une prédiction finale. Il n’a qu’un rôle d’arbitrage, et utilise par convention une fonction de transfert identité (x Æ x).
On peut se représenter l’action des neurones cachés comme une division de l’information entrante : sur certaines plages de valeurs, un seul neurone caché fournit une réponse utile à la prédiction, pendant que les autres ont un rôle neutre.
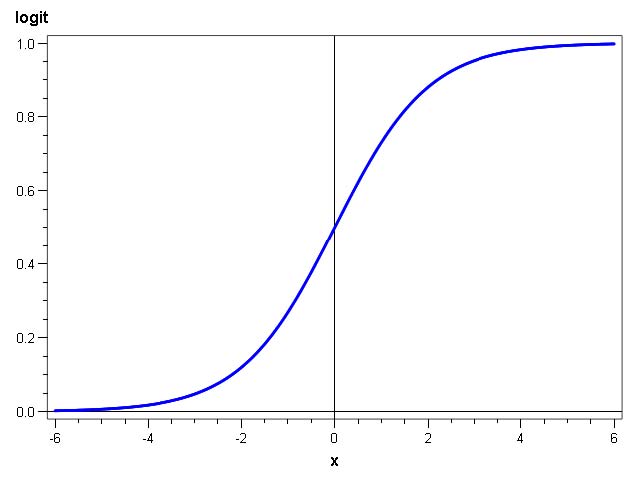
Dans une gamme particulière de réseaux, les Perceptrons Multi-Couches (PMC), la fonction de transfert des neurones cachés est une fonction à saturation, ou sigmoïde (c’est-à-dire en forme de S).
Etant donné que ces fonctions ne font pas de pics locaux pour redevenir nulles ensuite, l’activation d’un neurone caché devra être compensée par les autres neurones cachés. S’ensuit, lors de la mise au point du modèle, un grand jeu de compensations qui ralentit grandement la convergence vers un modèle optimal. Cependant, celui-ci présente de grandes garanties en termes de performance et de robustesse (c’est-à-dire de reproductibilité des performances sur des données
différentes).
Les choix architecturaux à faire a priori de la construction du modèle sont :
• le nombre de neurones cachés (moins il y en a, plus le modèle est robuste ; plus il y en a, plus il est performant) ;
• la fonction d’activation des neurones cachés (n’importe quelle fonction sigmoïde fait l’affaire, les performances étant très proches quelle que soit la fonction retenue).
Dans notre étude, la fonction tangente hyperbolique a été tout le temps utilisée. Un programme SAS se charge d’essayer toutes les architectures en faisant varier le nombre de neurones cachés entre un minimum (2) et un maximum (15 ou 20 selon le nombre d’informations entrantes) pour retenir le plus performant sur un jeu de test.
Enfin, on parle de linéarité quand des liaisons (et des poids synaptiques) existent entre les variables explicatives (carrés de gauche sur la Figure 2) et le neurone de sortie (dernier à droite). En effet, de telles liaisons permettent d’ajouter à la prédiction une partie linéaire : on intègre une régression linéaire en plus des qualités non-linéaires du réseau de neurones. Cependant, l’ajout de liaisons et donc de coefficients au modèle, s’il permet de gagner en performance, fait parfois perdre en robustesse, et la présence de liaisons directes n’est donc pas forcément souhaitable.
Avoir toujours raison, une fausse bonne idée
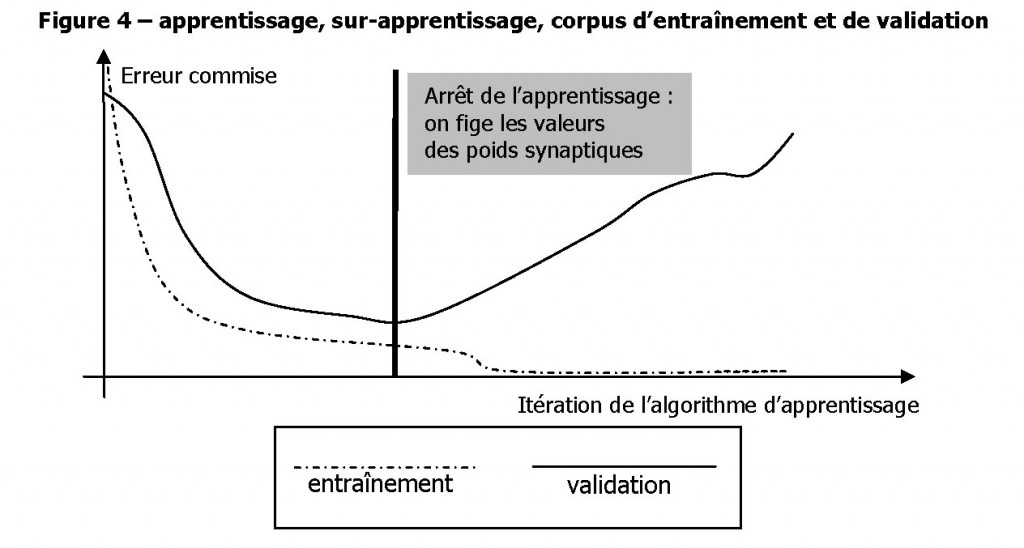
Il est dangereux de poursuivre indéfiniment la phase d’apprentissage sans contrôle : la capacité d’ajustement d’un réseau de neurones est tellement forte qu’au bout d’un certain nombre d’itérations, les poids synaptiques parviennent à prédire quasiment sans erreur les données.
A ce stade, en fait, le réseau de neurones ne se trompe plus dans ses prédictions, mais il y a un très grand risque pour que ces prédictions ne soient justes que pour les données sur lesquelles l’apprentissage s’est basé. On parle alors d’apprentissage par cœur ou de sur-apprentissage. On prévient l’apprentissage par cœur en divisant les données en deux : un jeu d’entraînement et un jeu de validation.
Les données d’entraînement sont celles qui vont servir à l’algorithme qui définit les meilleures valeurs des poids synaptiques. Les données de validation sont neutres dans la détermination des poids ; elles ne servent qu’à arrêter l’apprentissage à une itération précédent le début du surapprentissage. Cela permet de placer intuitivement cette limite, et illustre le rôle joué en pratique par les données de validation.
Les réseaux de neurones, une panacée ?
On pourrait penser que les réseaux de neurones sont les meilleurs modèles qu’on puisse imaginer, puisqu’ils sont performants et robustes à la fois.
Cependant, une troisième qualité d’un modèle est sa lisibilité, et là, les réseaux de neurones pèchent franchement : l’équation qui lie les informations entrantes aux prédictions existe, mais elle est tellement complexe (c’est une somme pondérée de fonctions sigmoïdes dont les arguments sont eux-mêmes pondérés !) qu’il est impossible d’isoler l’influence d’une variable explicative sur les prédictions du modèle.
Il est possible, par simulation, d’obtenir des indications sur le sens et l’ampleur de l’impact de certaines informations sur les prévisions réalisées par le réseau, mais une telle étude est très empirique, pour des résultats non garantis.