Principe géométrique de l’analyse discriminante linéaire
Ce qu’on cherche :
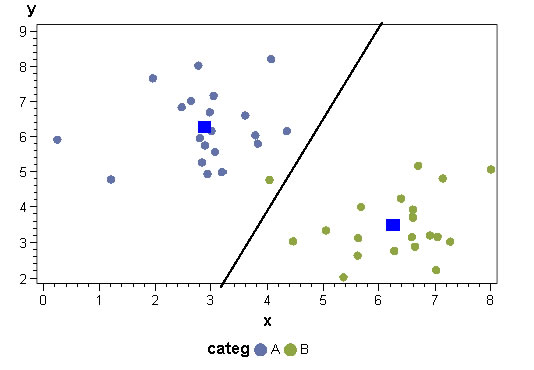
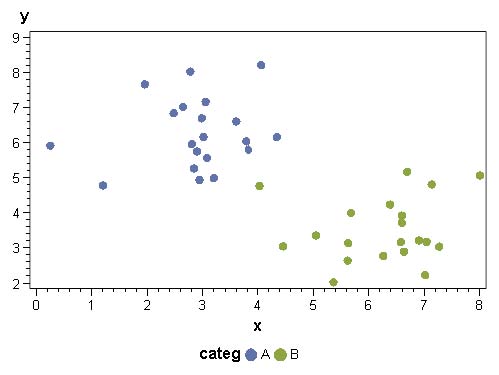
Une droite (un hyperplan / une séparation linéaire) entre deux groupes d’observations. Cette droite est une combinaison linéaire des variables explicatives, toutes continues, qui décrivent les deux groupes d’observations.
Comment on s’y prend :
Chacun des deux groupes d’observations est « remplacé » (synthétisé) par son barycentre (point de coordonnées moyennes de toutes les variables explicatives). La séparation entre les deux populations est faite selon une droite perpendiculaire au segment reliant les deux barycentres. Le point « zéro » (intersection droite / segment) est situé à une distance des barycentres qui dépend du nombre d’observations dans chaque groupe ; pour un échantillon équilibré, la droite séparatrice est équidistante des deux barycentres. Si un échantillon est 2 fois plus représenté que l’autre, l’intersection avec la droite sera située au 1/3 du segment, plus proche du barycentre de la population la plus nombreuse.
Principe statistique de l’analyse discriminante linéaire
Ce qu’on cherche :
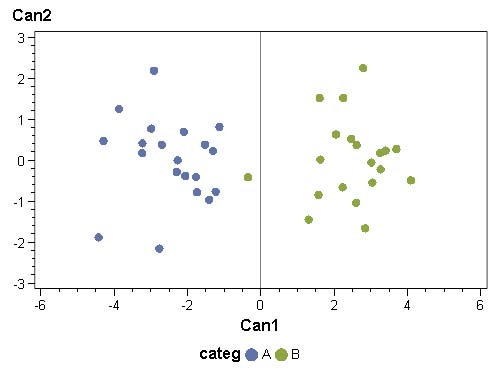
Un ensemble d’axes qui résument au mieux la distance existant entre deux groupes d’observations. Dans ce nouveau repère, les points des deux groupes doivent être aussi distants les uns des autres que possibles, et aussi proches que possible les uns des autres au sein d’un même groupe.
Comment on s’y prend :
La variabilité (variance) de deux groupe d’observations est la somme de deux composantes : sa variance intra-groupe (éloignement moyen du barycentre) Vintra, et la variance inter-groupes (éloignement des deux barycentres) Vinter. Les deux composantes s’additionnent pour donner la variance totale de l’ensemble des deux groupes d’observations : Vintra + Vinter = Vtotale (théorème de Huyguens).
On peut donc chercher un ensemble d’axes qui résume au mieux la variance intergroupes (c’est-à-dire qui disperse au maximum les observations si elles appartiennent à deux groupes différents) et qui, dans le même temps (puisque les deux sont liées), minimise la variance intra-groupe (c’est-à-dire représente toutes proches les observations d’un même groupe).
Le jeu d’axes à obtenir correspond à une analyse en correspondances principales (ACP) de la matrice de variance inter-groupes. Les axes factoriels qui en proviennent (vecteurs propres de la matrice) sont des droites le long desquels on projette deux points :
• loin l’un de l’autre s’ils appartiennent à deux groupes différents ;
• près l’un de l’autre s’ils appartiennent au même groupe.
Ce qu’on obtient dans les deux cas
On obtient p-1 axes discriminants si on cherche à séparer p groupes. Les coordonnées des axes discriminants (appelés « fonctions linéaires discriminantes » ou « fonctions discriminantes de Fisher ») sont fournies : elles correspondent au nouveau jeu d’axes factoriels (approche statistique) et à l’équation du segment reliant les deux barycentres (approche géométrique). Le signe d’une projection (coordonnées sur ce nouveau jeu d’axes) est une convention, mais détermine dans quelle catégorie une observation sera prédite.
Hypothèses de l’analyse discriminante linéaire
• Indépendance des observations (pour avoir des matrices de variance/covariance faciles à séparer en variance inter et variance intra)
• Normalité des variables explicatives.
Il n’est pas nécessaire d’avoir des variables explicatives indépendantes, car la construction des facteurs discriminants (le nouveau repère dans lequel on regarde les points pour y séparer au mieux les catégories) s’affranchit d’éventuelles
corrélations.
En revanche, la normalité est demandée, et il est souvent difficile de l’obtenir pour toutes les variables descriptives. Une relative robustesse de la méthode fait que l’on peut employer des variables qui, à défaut de suivre exactement une loi normale, sont unimodales (un seul pic de valeur dans leurs distributions) et à peu près symétriques.
L’analyse discriminante sur données qualitatives (méthode DISQUAL)
Les hypothèses ci-dessus sont impossibles à satisfaire si on possède au moins une variable explicative qualitative. On peut alors procéder de la manière suivante :
1. Transformation de TOUTES les variables explicatives en variables qualitatives (mise en classes). De préférence, on construira des variables avec le même nombre de modalités et des effectifs assez proches au sein de chaque modalité. Cependant, l’emploi de quantiles n’est pas forcément une solution optimale pour la qualité du modèle.
2. Construction d’axes factoriels à l’aide d’une Analyse en Composantes Multiples (ACM) ; ces axes sont des variables quantitatives, unimodales et symétriques. Ils satisfont donc les hypothèses énoncées plus haut.
3. Analyse discriminante linéaire sur les axes factoriels. Les coefficients obtenus pour la fonction de Fisher s’appliquent aux axes ; mais comme ceux-ci sont eux-mêmes des combinaisons linéaires des indicatrices des variables d’origine, il est aisé (par produit matriciel) de retrouver les valeurs des coefficients de la fonction linéaire discriminante sur les variables d’origine.
Outre son intérêt immédiat de pouvoir traiter tout type de variable explicative en ne nécessitant éventuellement qu’un recodage en classes, DISQUAL permet également quelques progrès par rapport à l’analyse discriminante classique.
FILTRAGE DE L’INFORMATION NON UTILE :
• Soit au niveau des axes factoriels produits par l’ACM, en ne retenant que les X premiers axes qui représentent une fraction fixée d’avance de la variance initiale des données. Attention, on élimine ici du bruit statistique sur l’ensemble des informations décrivant les données, et pas de l’information inutile à la modélisation.
• Soit au niveau des axes factoriels à utiliser pour l’analyse discriminante (procédure STEPDISC de SAS permettant de ne sélectionner que les variables explicatives augmentant la part de variance inter-groupes expliquée de manière significative).
Ces deux filtres peuvent être combinés pour construire des modèles qui seront extrêmement robustes, mais nettement moins performants d’une modélisation sans filtres.
RÉSULTATS :
• Dans les coefficients habituellement produits par l’analyse discriminante, les valeurs sont fonction de la variance de la variable associée. Dans DISQUAL, les coefficients sur variables d’origine sont tous directement comparables, puisqu’ils représentent tous des indicatrices (dont les variances sont constantes si elles représentent des nombres de groupes assez proches). La valeur absolue d’un coefficient permet donc de mesurer directement l’impact de la caractéristique associée sur le phénomène à modéliser.
• Comme toutes les variables explicatives sont qualitatives, le score produit (la valeur de la fonction de Fisher) sera borné entre la pire et la meilleure combinaison de caractéristiques. On peut donc « recadrer » les coefficients pour obtenir un score compris entre 0 et 1. Les résultats de DISQUAL sont alors comparables à ceux des autres modélisations comme les régressions logistiques, les arbres de décision ou les réseaux de neurones. Entre autres, on peut sur tous construire des courbes ROC, des courbes de lift, etc.