Pour améliorer un graphique SAS, il n’est forcément payant de passer des heures à éplucher la documentation pour trouver une option magique. Il est souvent plus simple de donner à SAS des instructions de dessin pour qu’il surcharge la version « brute » du graphique. Ces instructions de dessin sont consignées dans une table appelée Annotate ; pour faire des merveilles, il suffit généralement d’une étape Data et d’un peu d’organisation.
Comment se présente une table Annotate ?
Il s’agit d’une table SAS tout à fait normale, qui intègre des variables aux noms normalisés.
• X et Y indiquent quelles sont les positions horizontale et verticale de l’élément dessiné dans le graphique. X et Y ne peuvent avoir que des valeurs numériques ; si le graphique est en bâtons ou en camembert, alors il faudra utiliser une variable XC qui prend des valeurs caractères.
• FUNCTION indique le type d’élément graphique à ajouter. Nous revenons ci-dessous sur les principales valeurs de cette variable.
• WHEN (valant « A » ou « B ») indique quand l’élément doit être ajouté au graphique : avant (valeur B comme Before) ou après (valeur A comme After) le dessin par la procédure graphique principale (GPLOT ou GCHART).
• XSYS et YSYS indiquent dans quelle unité de mesure sont données les valeurs des variables X/XC et Y/YC. On utilise le plus souvent la valeur « 2 » (les variables XSYS et YSYS sont obligatoirement de type caractère) qui font référence aux unités des
axes du graphique. On peut aussi utiliser la valeur « 3 » qui exprime X et Y en pourcentages de l’ensemble de la fenêtre graphique.
• Ainsi que d’autres variables (TEXT, POSITION, COLOR, SIZE, STYLE, ANGLE, MIDPOINT, …) qui dépendent de la fonction graphique (variable FUNCTION) sélectionnée.
Chaque observation correspond à une action à effectuer : le principe est le même que pour les « tables traçantes » des années 80.
FUNCTION = « MOVE » : on se contente de déplacer le curseur graphique sans tracer quoi que ce soit. Utile pour le cas FUNCTION = « DRAW » qui trace une droite du point où se trouvait précédemment le curseur jusqu’au nouveau point. Un tracé de segment correspond donc à deux observations : MOVE avec les coordonnées d’une extrémité, puis DRAW avec les coordonnées de l’autre extrémité.
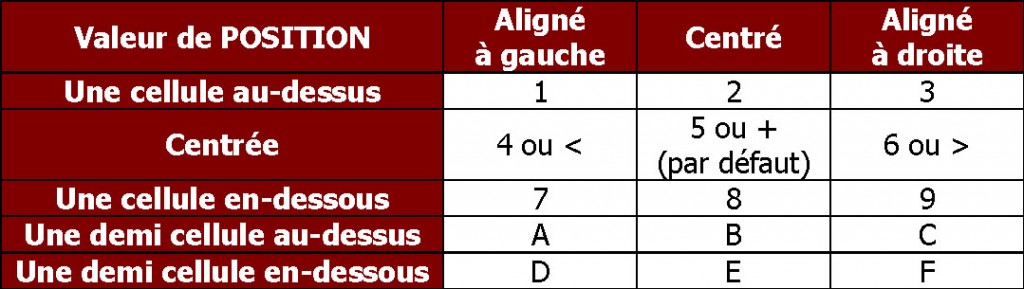
FUNCTION = « LABEL » : on affiche un texte contenu dans la variable TEXT. La variable POSITION indique l’emplacement du texte par rapport au point de coordonnées X,Y. Il y a 16 valeurs pour POSITION, toujours de type caractère.
FUNCTION = « BAR » : on dessine un rectangle dont le coin inférieur gauche se trouve à l’emplacement précédent du curseur, et le coin supérieur droit à l’emplacement actuel du curseur. Comme pour les segments, le dessin d’un rectangle se fait sur deux observations, l’une MOVE et l’autre BAR. La variable COLOR indique la couleur pour l’intérieur du rectangle si STYLE= « S », et la couleur du trait extérieur si STYLE= « E » (le rectangle est alors sans contenu. La variable LINE permet d’indiquer : pour la valeur 0 qu’il y a une bordure extérieure au rectangle, et pour la valeur 3, qu’il n’y en a pas.
FUNCTION = « IMAGE » : on insère une image (chemin et nom donnés dans la variable IMAGEPATH) dont le coin inférieur gauche se trouve à l’emplacement précédent du curseur, et le coin supérieur droit à l’emplacement actuel du curseur. Le fonctionnement est le même que pour BAR ou DRAW : MOVE à une première observation, puis IMAGE à une seconde. La variable STYLE vaut « TILE » si l’image doit être insérée à sa vraie taille, en mode mosaïque, ou « FIT » si l’image doit être adaptée aux dimensions de l’aire rectangulaire.
FUNCTION = « SYMBOL » : on insère un marqueur graphique, identique à ceux que propose la procédure GPLOT. TEXT est la variable qui indique quel est le marqueur, tandis que COLOR et SIZE régissent son apparence.
FUNCTION = « PIE » : on dessine un cercle ou une portion de cercle dans le graphique. Attention, si les deux axes du graphique ne sont pas gradués à l’identique, le cercle ne sera pas déformé en ovale (voir exemple 2). La variable ROTATE indique quel angle (en degrés) fait la portion de cercle. La variable ANGLE indique d’où part l’arc de cercle, en degrés par rapport à l’horizontale, dans le sens trigonométrique (sens inverse des aiguilles d’une montre). La variable SIZE donne le rayon du cercle, dans une unité déterminée dans la variable HSYS (généralement, « 2 » : les unités des axes du graphique). La variable LINE permet de dessiner un arc de cercle, une portion de cercle, ou un hybride des deux.
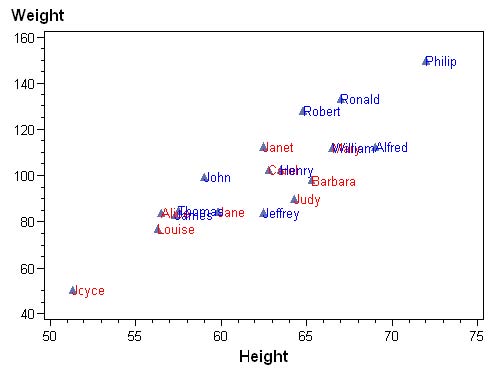
Exemple n°1 : ajouter des labels à des points
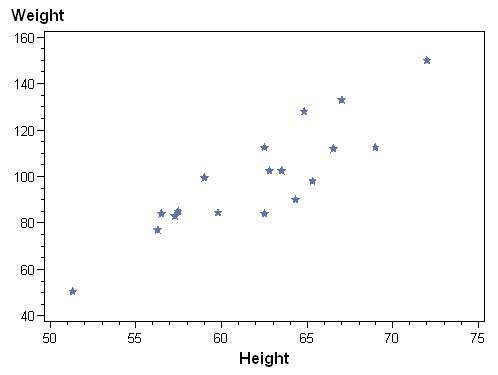
Dans cet exemple, nous utilisons les données exemple de SAS, la table SASHELP.CLASS.
Le graphique de base se présente ainsi.
SYMBOL I = NONE V = STAR ;
PROC GPLOT
DATA = sashelp.class ;
PLOT weight * height ;
RUN ; QUIT ;
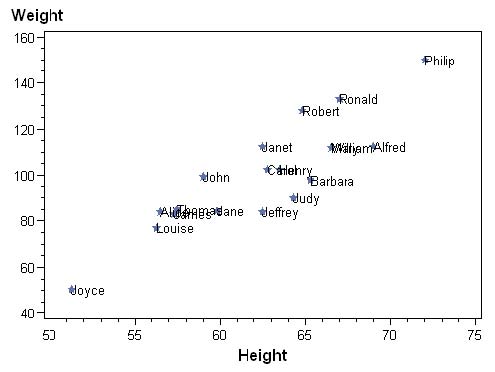
On souhaite ajouter les prénoms des enfants à côté de chaque point.
DATA work.labels ;
SET sashelp.class ;
xsys = "2" ;/* abscisses : unités des axes */
ysys = "2" ;/* ordonnées : unités des axes */
when = "A" ;/* ajouter APRES la procédure */
function = "LABEL" ; /* on écrit un texte */
text = name ; /* ce texte = le contenu de NAME */
position = ">" ; /* aligné à gauche sur le point */
x = height ; /* mêmes coordonnées que les points */
y = weight ;
RUN ;
PROC GPLOT DATA = sashelp.class ;
PLOT weight * height / ANNOTATE = work.labels ;
RUN ; QUIT ;
Si on veut avoir des libellés de couleur différente pour filles et garçons, il suffit d’aménager l’étape Data.
DATA work.labels ;
SET sashelp.class ;
xsys = "2" ; ysys = "2" ;
when = "A" ; function = "LABEL" ;
x = height ; y = weight ;
text = name ; position = ">" ;
IF sex="F" THEN color = "RED " ;
ELSE color = "BLUE" ;
RUN ;
PROC GPLOT DATA = sashelp.class ;
PLOT weight * height / ANNOTATE = work.labels ;
RUN ; QUIT ;
Exemple n°2 : plan factoriel d’ACP et cercle des corrélations
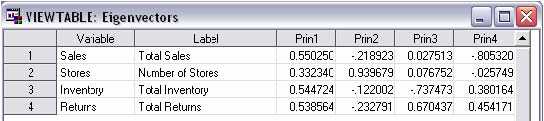
A partir des données de la table exemple SASHELP.SHOES, nous allons résumer les 4 variables numériques qui s’y trouvent dans le premier plan factoriel d’une ACP.
ODS OUTPUT eigenvectors = work.vecteurs_propres ;
PROC PRINCOMP DATA = sashelp.shoes ;
VAR sales stores inventory returns ;
RUN ;
On récupère avec ce code les coordonnées des variables d’origine dans le premier plan factoriel.
La table produite a l’aspect suivant :
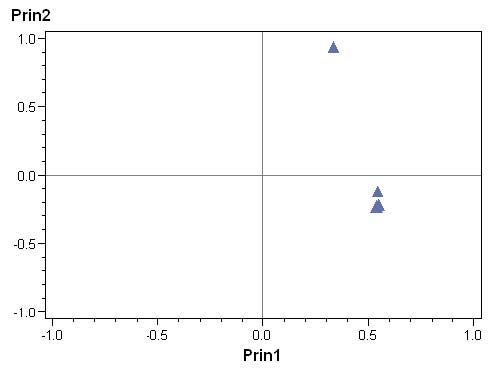
Dans le plan factoriel des variables, il est usuel de représenter chacune des variables d’origine comme une flèche partant du point 0,0 et inscrite à l’intérieur d’un cercle de rayon 1 et de centre 0,0.
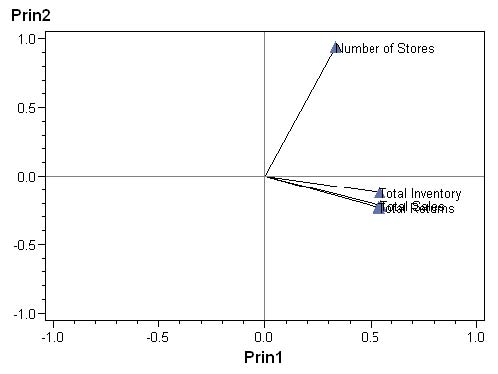
Commençons par la base : afficher les points via une procédure
GPLOT. SYMBOL i = none v = triangle ;
PROC GPLOT DATA = work.vecteurs_propres ;
PLOT prin2 * prin1 / HREF = 0
VREF = 0
HAXIS = -1 TO 1 BY .5
VAXIS = -1 TO 1 BY .5 ;
RUN ; QUIT ;
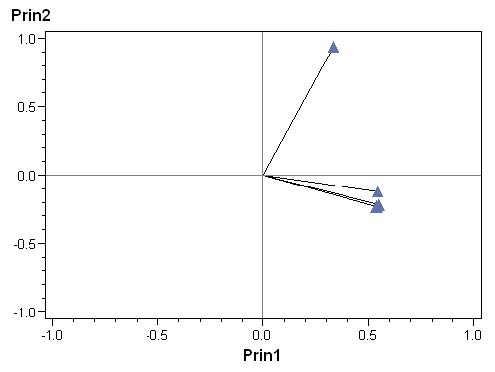
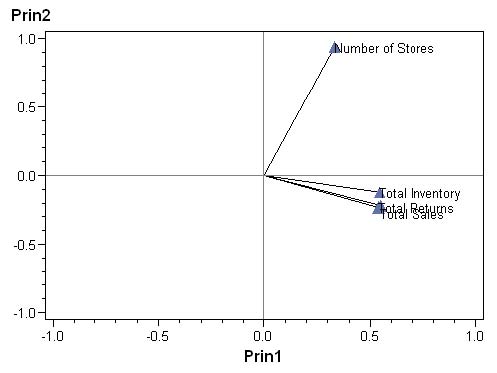
La première partie de la table Annotate consiste à tracer les segments allant du centre du graphique à chacun des points.
DATA work.anno_acp ;
SET work.vecteurs_propres ;
xsys = "2" ; ysys = "2" ;
LENGTH function $ 8 ;
when = "B" ;
x = 0 ;
y = 0 ;
function = "MOVE" ;
OUTPUT ;
x = prin1 ;
y = prin2 ;
function = "DRAW" ;
OUTPUT ;
RUN ;
SYMBOL i = none v = triangle ;
PROC GPLOT DATA = work.vecteurs_propres
ANNOTATE = work.anno_acp ;
PLOT prin2 * prin1 / HREF = 0
VREF = 0
HAXIS = -1 TO 1 BY .5
VAXIS = -1 TO 1 BY .5 ;
RUN ; QUIT ;
DATA work.anno_acp ;
SET work.vecteurs_propres ;
xsys = "2" ; ysys = "2" ;
LENGTH function $ 8 ;
when = "B" ;
x = 0 ;
y = 0 ;
function = "MOVE" ;
OUTPUT ;
x = prin1 ;
y = prin2 ;
function = "DRAW" ;
OUTPUT ;
when = "A" ; position = ">" ;
function = "LABEL" ;
text = COALESCEC(label,variable) ;
OUTPUT ;
RUN ;
On ajoute ensuite la fonction LABEL pour agrémenter les points du label ou du nom de la variable ; la fonction SAS COALESCEC (nouvelle avec SAS 9) permet d’attribuer la valeur d’une variable, et si celle-ci est manquante, la valeur d’une seconde variable. On a ici, soit le label s’il existe, soit le nom de la variable comme libellé de point.
Afin d’éviter le chevauchement de libellés des deux derniers points, on peut prévoir un ajustement “à la main”.
Il est très difficile d’anticiper automatiquement les chevauchements, étant donné qu’ils peuvent se produire sur un plan horizontal ou vertical.
when = "A" ; function = "LABEL" ; text = COALESCEC(label,variable) ; IF UPCASE(variable) NE "SALES" THEN position = ">" ; ELSE position = "9" ; OUTPUT ;
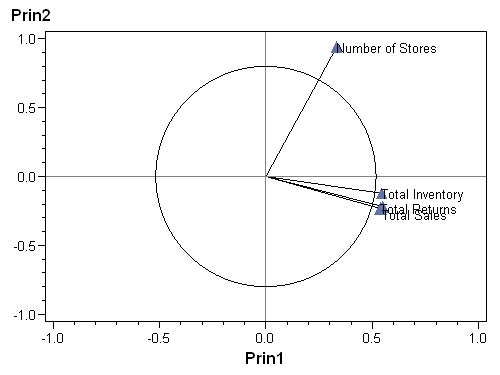
Reste à ajouter le cercle des corrélations. La fonction PIE ne fournit pas vraiment une bonne solution, puisqu’elle dessine un véritable cercle, là où l’asymétrie des axes devrait afficher une ellipse.
DATA work.anno_acp ;
SET work.vecteurs_propres END = fin ;
xsys = "2" ; ysys = "2" ;
LENGTH function $ 8 ;
when = "B" ;
x = 0 ;
y = 0 ;
function = "MOVE" ;
OUTPUT ;
x = prin1 ;
y = prin2 ;
function = "DRAW" ;
OUTPUT ; when = "A" ;
function = "LABEL" ;
text = COALESCEC(label,variable) ;
IF UPCASE(variable) NE "SALES" THEN position = ">" ;
ELSE position = "9" ;
OUTPUT ;
IF fin THEN DO ;
x = 0 ;
y = 0 ;
when = "A" ;
hsys = "2" ;
function = "PIE" ;
size = 1 ;
angle = 0 ;
rotate = 360 ;
OUTPUT ;
END ;
RUN ;
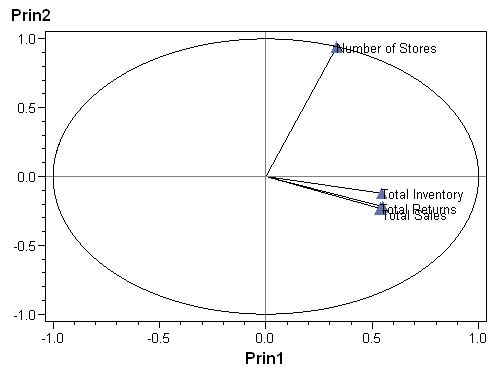
Reste une solution plus radicale, mais plus adaptée à notre problème : dessiner un à un les points qui composent le cercle. Leur abscisse est cosinus d’un angle, leur ordonnée, le sinus du même angle. On a donc « juste » à boucler sur toutes les valeurs (un peu plus de 600 points) d’un angle allant de 0 à 2 pi radians.
DATA work.anno_acp ;
SET work.vecteurs_propres END = fin ;
xsys = "2" ; ysys = "2" ;
LENGTH function $ 8 ;
when = "B" ;
x = 0 ;
y = 0 ;
function = "MOVE" ;
OUTPUT ;
x = prin1 ;
y = prin2 ;
function = "DRAW" ;
OUTPUT ;
when = "A" ;
function = "LABEL" ;
text = COALESCEC(label,variable) ;
IF UPCASE(variable) NE "SALES" THEN position = ">" ;
ELSE position = "9" ;
OUTPUT ;
IF fin THEN DO ;
x = 1 ;
y = 0 ;
when = "A" ;
function = "MOVE" ;
OUTPUT ;
DO angle = 0 TO 2*3.14 BY 0.01 ;
function = "DRAW" ;
x = COS(angle) ;
y = SIN(angle) ;
OUTPUT ;
END ;
x = 1 ;
y = 0 ;
function = "DRAW" ;
OUTPUT ;
END ;
RUN ;
Exemple n°3 : superposition dans un diagramme en bâtons
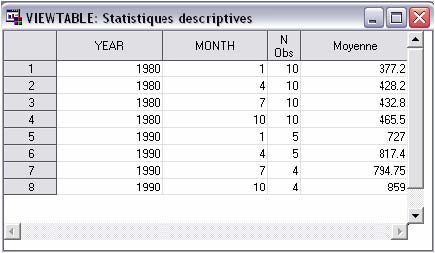
Dans cet exemple, nous utilisons les données exemple de SAS, la table SASHELP.RETAIL. Les données sont pré-agrégées par une procédure MEANS.
PROC FORMAT ; VALUE decennies 1980-1989 = "80's" 1990-1999 = "90's" ; RUN ; ODS OUTPUT summary = work.ventes ; PROC MEANS DATA = sashelp.retail MEAN ; VAR sales ; CLASS year month ; FORMAT year decennies. ; RUN ;
Voici la table VENTES créée à l’issue de ce traitement.
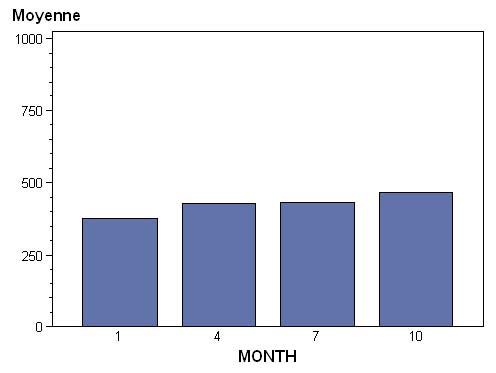
A partir de cette table, on représente, par trimestre, la moyenne des ventes pour l’ensemble des années 80.
Le graphique de base se présente ainsi.
AXIS1 ORDER = (0 TO 1000 BY 250) ; PROC GCHART DATA = work.ventes ; WHERE year = 1980 ; VBAR month / DISCRETE SUMVAR = sales_mean TYPE = MEAN RAXIS = axis1 ; RUN ; QUIT ;
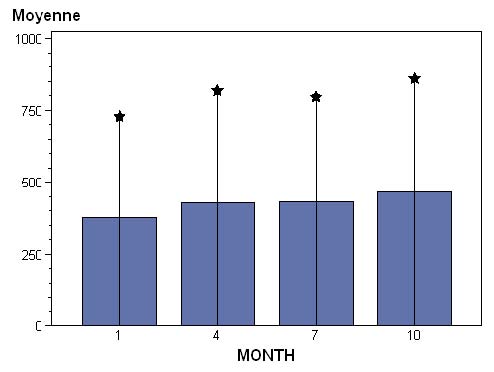
Cette table Annotate permet de voir l’utilité de la variable MIDPOINT. Elle ne s’utilise que pour les diagrammes en bâtons. On peut utiliser la variable X de manière totalement équivalente.
DATA work.annees90 ;
SET work.ventes ;
WHERE year = 1990 ;
xsys = "2" ; ysys = "2" ;
when = "A" ;
midpoint = month ;
function = "MOVE " ;
y = 0 ;
OUTPUT ;
function = "DRAW " ;
y = sales_mean ;
OUTPUT ;
function = "SYMBOL" ;
text = "STAR" ;
OUTPUT ;
RUN ;
FOOTNOTE1 "* = années 90 ; barres = années 80" ;
PROC GCHART DATA = work.ventes ANNOTATE = work.annees90 ;
WHERE year = 1980 ;
VBAR month / DISCRETE
SUMVAR = sales_mean
TYPE = MEAN
RAXIS = axis1 ;
RUN ; QUIT ;
FOOTNOTE ;
* = années 90 ; barres = années 80